# Part ONE: Review the approach to location and scale problems for one and two populations
For inference on population mean, which of the following could we potentially use? Choose all apply
For inference on population mean when population variance is known, which of the following should we use? (In this part, suppose X_1, ... , X_1000 is a random sample (of size 1000) from some unknown distribution.)
For inference on population mean when population variance is unknown, which of the following should we use? (In this part, suppose X_1, ... , X_1000 is a random sample (of size 1000) from some unknown distribution.)
For inference on population variance, which of the following distributions will be useful?
For comparing variances between two populations, which of the following distributions will be useful?
# Part Two: Confidence Interval and Hypothesis Testing (35 points)
# Problem 1.
An electrical firm manufactures light bulbs that have a length of life that is approximately normally distributed, with mean equal to 800 hours and a standard deviation of 40 hours. A random sample of 16 bulbs will have an average life of less than 775 hours. (15 points)
a. Give a probabilistic result that indicates how rare an event is when . On the other hand, how rare would it be if truly were, say, 760 hours?
By Central Limit Theory, we know when n is large,
nsize <- 16 # Sample Size | |
sigma <- 40/sqrt(nsize) # Sample standard deviation | |
mu <- 800 # Sample mean | |
p <- pnorm(775, mean = mu, sd = sigma) | |
p | |
mu <- 760 # if sample mean were 760 | |
p <- pnorm(775, mean = mu, sd = sigma) | |
p |
[1] 0.006209665
[1] 0.9331928
# mu = 800, P(xbar<=775) | |
pnormGC(775, mean =800, sd =40/sqrt(16), graph = TRUE) |
[1] 0.006209665

# mu = 760, P(xbar<=775) | |
pnormGC(775, mean =760, sd =40/sqrt(16), graph = TRUE) |
[1] 0.9331928

Conclusion: When ; however, . This tells us based on the sample that it is more likely should be 760 instead of 800.
b. Please construct a 95% confidence interval on with . Is 800 inside the interval?
alpha <- 0.05 | |
zalpha2 <- qnorm(1-alpha/2) | |
sd <- 40 | |
n <- 16 | |
xbar <- 775 | |
loBd <- xbar-zalpha2*sd/sqrt(n) | |
loBd |
[1] 755.4004
upBd <- xbar+zalpha2*sd/sqrt(n) | |
upBd |
[1] 794.5996
Conclusion: 95% confidence interval is (755.4,794,6). 800 is not inside the interval.
c. We wish to test
Will you reject suppose ? Justify your answer.
. We want to calculate zvalue first. If consider = 0.05%, the reject region is
z <- (xbar-800)/(sd/sqrt(n)) | |
z |
[1] -2.5
#pvalue | |
2*pnormGC(z) |
[1] 0.01241933
We can find and p-value < 0.05, therefore, we should reject .
# Problem 2.
A maker of a certain brand of low-fat cereal bars claims that the average saturated fat content is 0.5
gram. In a random sample of 8 cereal bars of this brand, the saturated fat content was 0.6, 0.7, 0.7, 0.3, 0.4, 0.5, 0.4, and 0.2. Assume a normal distribution. (10 points)
Please construct a 95% confidence interval on the average saturated fat content.
Would you agree with the claim? Justify your answer.
We consider using t-test, as we don’t know the variance.
fat <-c(0.6, 0.7, 0.7, 0.3, 0.4, 0.5, 0.4, 0.2) | |
t.test(fat,alternative = c("two.sided"), mu = 0.5, conf.level = 0.95) |
One Sample t-test
data: fat
t = -0.38592, df = 7, p-value = 0.711
alternative hypothesis: true mean is not equal to 0.5
95 percent confidence interval:
0.32182 0.62818
sample estimates:
mean of x
0.475
Base on the results, we find the 95% confidence interval is (0.32182,0.62818) and p value is much larger than 0.05. We should not reject .
# Problem 3. Checking out some small data sets that come with R (10 points)
In this problem, you will load and work with the mtcars data set in R.
Two data samples are independent if they come from unrelated populations and the samples does not affect each other. Here, we assume that the data populations follow the normal distribution.
In the data frame column mpg (which stands for "miles per galon") of the data set mtcars , there are gas mileage data of various 1974 U.S. automobiles. Let's take a look:
mtcars$mpg |
[1] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4
[16] 10.4 14.7 32.4 30.4 33.9 21.5 15.5 15.2 13.3 19.2 27.3 26.0 30.4 15.8 19.7
[31] 15.0 21.4
Meanwhile, another data column in mtcars , named am , indicates the transmission type of the automobile model (0 = automatic, 1 = manual):
mtcars$am |
[1] 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 1 1 1 1 1
In particular, the gas mileage for manual and automatic transmissions are two independent data populations.
Assume that the data in mtcars follows the normal distribution, let us look for whether the difference between the mean gas mileage of manual and automatic transmissions seems to be statistically significant.
Hints and shortcuts The gas mileage for automatic transmission can be listed as follows:
L = mtcars$am == 0 | |
mpgAuto = mtcars[L,]$mpg | |
mpgAuto # automatic transmission mileage |
[1] 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4 10.4 14.7 21.5
[16] 15.5 15.2 13.3 19.2
By applying the negation of L, we can find the gas mileage for manual transmission:
mpgManual = mtcars[!L,]$mpg | |
mpgManual # manual transmission mileage |
[1] 21.0 21.0 22.8 32.4 30.4 33.9 27.3 26.0 30.4 15.8 19.7 15.0 21.4
a. Please construct a hypothesis test for ratio of the variances of these two populations. Then choose the appropriate test to make a conclusion.
The hypothesis testing should be
# alpha = 0.05 | |
var.test(mpgAuto,mpgManual,alternative = c("two.sided"),conf.level = 0.95) |
F test to compare two variances
data: mpgAuto and mpgManual
F = 0.38656, num df = 18, denom df = 12, p-value = 0.06691
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.1243721 1.0703429
sample estimates:
ratio of variances
0.3865615
# alpha = 0.1 | |
var.test(mpgAuto,mpgManual,alternative = c("two.sided"),conf.level = 0.9) |
F test to compare two variances
data: mpgAuto and mpgManual
F = 0.38656, num df = 18, denom df = 12, p-value = 0.06691
alternative hypothesis: true ratio of variances is not equal to 1
90 percent confidence interval:
0.1505051 0.9053528
sample estimates:
ratio of variances
0.3865615
If we consider , we can not reject . However, if , based on the result, we should consider to reject .
b. Based on the result in a), construct a hypothesis test for the means of these two populations. Show your conclusion.
The hypotheis test is
If we consider , we have the variances are the same. Thus we use the condition variances are equal but unknown.
t.test(mpgAuto,mpgManual,alternative = c("two.sided"), var.equal = TRUE, conf.level = 0.95) |
Two Sample t-test
data: mpgAuto and mpgManual
t = -4.1061, df = 30, p-value = 0.000285
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-10.84837 -3.64151
sample estimates:
mean of x mean of y
17.14737 24.39231
However, if we choose , we should use the condition variances are not equal.
t.test(mpgAuto,mpgManual,alternative = c("two.sided"), var.equal = FALSE, conf.level = 0.9) |
Welch Two Sample t-test
data: mpgAuto and mpgManual
t = -3.7671, df = 18.332, p-value = 0.001374
alternative hypothesis: true difference in means is not equal to 0
90 percent confidence interval:
-10.576623 -3.913256
sample estimates:
mean of x mean of y
17.14737 24.39231
No matter what value of , based on the result, we should reject .
# Part Three: Working With Data (50 points)
# Instructions: Please review EDA Handout first. Import the needed packages first.
- Obtaining the adult dataset
# Tasks
For the following exercises, work with the adult.data data set. Use either Python or R to solve each
problem. Please read the adult.name file to understand each attribute.
a. Import the adult.data data set and name it adult . (5 points)
adult <- read.csv("adult.data", header=FALSE) | |
# View(adult) |
To make the plot better, we rename all the attributes.
names(adult)[1:15] <- c("age","workclass", "fnlwgt", "education","education-num","marital-status","occupation","relationship","race","sex","capital-gain","capital-loss","hours-per-week","native-country","class(response)") |
b. Standardize hours-per-week and indicate if there is any outlier (5 points)
hrsWeek_z <- scale(adult$`hours-per-week`) | |
adult_outliers <- adult[hrsWeek_z < -3| hrsWeek_z>3,] | |
#too many outliers, just show the first six records | |
head(adult_outliers) |
age workclass fnlwgt education education-num
11 37 Private 280464 Some-college 10
29 39 Private 367260 HS-grad 9
78 67 ? 212759 10th 6
158 71 Self-emp-not-inc 494223 Some-college 10
190 58 State-gov 109567 Doctorate 16
273 50 Self-emp-not-inc 30653 Masters 14
marital-status occupation relationship race sex
11 Married-civ-spouse Exec-managerial Husband Black Male
29 Divorced Exec-managerial Not-in-family White Male
78 Married-civ-spouse ? Husband White Male
158 Separated Sales Unmarried Black Male
190 Married-civ-spouse Prof-specialty Husband White Male
273 Married-civ-spouse Farming-fishing Husband White Male
capital-gain capital-loss hours-per-week native-country class(response)
11 0 0 80 United-States >50K
29 0 0 80 United-States <=50K
78 0 0 2 United-States <=50K
158 0 1816 2 United-States <=50K
190 0 0 1 United-States >50K
273 2407 0 98 United-States <=50K
boxplot(adult$`hours-per-week`) |

Answer: Based the two methods, we can find there are a lot of outliers of
hours-per-week.
c. Show a bar graph of race with a response class overlay. What conclusion can you draw from the bar graph? (10 points)
table(adult$race,adult$`class(response)`) |
<=50K >50K
Amer-Indian-Eskimo 275 36
Asian-Pac-Islander 763 276
Black 2737 387
Other 246 25
White 20699 7117
ggplot(data = adult,mapping = aes(x =race, fill = `class(response)`)) + | |
geom_bar() |

ggplot(data = adult,mapping = aes(x =race, fill = `class(response)`))+ | |
geom_bar(position = "fill") |

If we don’t use
fill, we can findWhiteis dominated in theraceattribute. If we want to compare the percentage of>50kin each category, we should usefill. The interesting thing is the percentage of>50kinAsian-Pac-Islanderare competitive to the percentage inWhite. The other category actally has the lowest percentage.
d. Select any numeric attribute and show a histogram of it with a response class overlay. What conclusion can you draw from the histogram? (10 points)
I choose
hours-per-weekas the attribute.
ggplot(data = adult,mapping = aes(x =`hours-per-week`, fill = `class(response)`)) + geom_histogram(binwidth = 10) |

ggplot(data = adult,mapping = aes(x =`hours-per-week`, fill = `class(response)`)) + geom_histogram(binwidth = 10, color = "black",position = "fill") |

Here I use the
binwidthis 10. If you choose different options, the graph will be slightly different and the tendency will be the same. If we don’t usefill, it is easy to know working hours around 40 should dominate inhours-per-weekand about 25% in theclassof>50k. However, the highest percentage of>50koccurs at the working hours from 45 to 65 instead of the 40 bin. Someone can get>50kincome when they almost don’t work.
e. Select any two attributes and show a plot, what conclusion can you draw from the plot? (10 points)
Here, I choose
sexandclassas two attributes.
ggplot(data = adult, mapping = aes(x = `sex`,fill = `class(response)`)) + | |
geom_bar() |
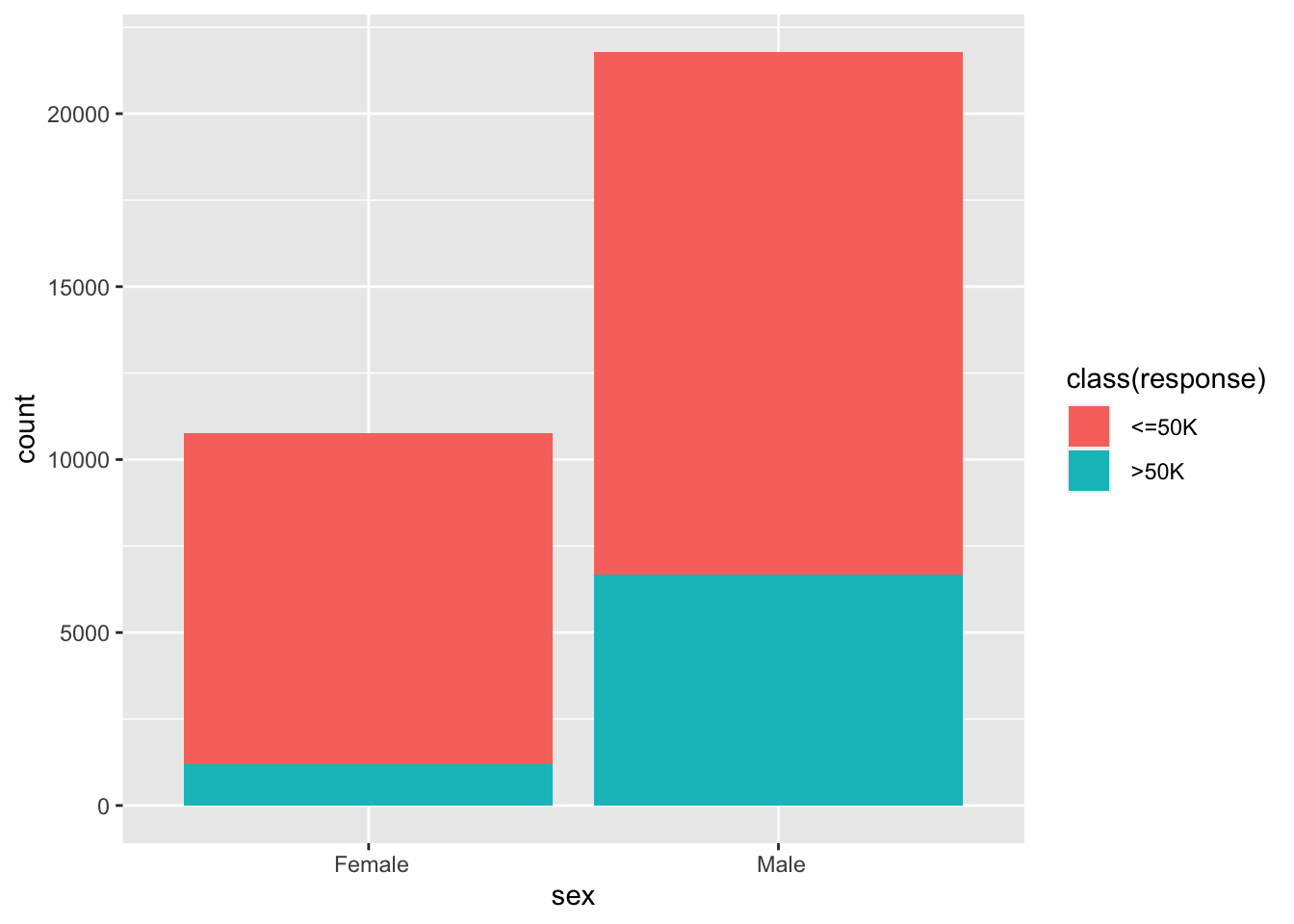
ggplot(data = adult, mapping = aes(x = `sex`,fill = `class(response)`)) + | |
geom_bar(position = 'fill') |

In this dataset, the number of male is almost double of the number of female. More than that, the percentage of
>50kfor male is almost triple of the percentage for female.
f. Select any three attributes and plot their relationship using 2D scatter plot, use one of the selected attributes as the color code when plotting, what can you say about the correlation of these attributes? What conclusion can you draw from the plot? (10 points)
Here, I choose
age,hours=per-week, andclassas the attributes.
ggplot(data = adult) + | |
geom_point(mapping = aes(x = age, y = `hours-per-week`,colour = `class(response)`)) |

If your age is less than 25, even you work 100 hrs per week, it is still difficult for you to make income
>50k. When you are older than 75, it is not easy for you to make>50k. The income is not proportional to thework-per-hours.
# Extra Points (10 points)
One claim "Female and Male have the same proportion >50k of the class ". Can you use what you learn in class to reject or fail to reject the statement? Justify your answer.
Hint: Need a proportion test here.
sexresponsetable<-table(adult$sex,adult$`class(response)`) | |
x11 <- sexresponsetable[1,1] | |
x12 <- sexresponsetable[1,2] | |
x21 <- sexresponsetable[2,1] | |
x22 <- sexresponsetable[2,2] | |
prop.test(x = c(x12,x22),n = c(x11+x12,x21+x22),conf.level = 0.95) |
2-sample test for equality of proportions with continuity correction
data: c out of cx12 out of x11 + x12x22 out of x21 + x22
X-squared = 1517.8, df = 1, p-value < 2.2e-16
alternative hypothesis: two.sided
95 percent confidence interval:
-0.2048416 -0.1877104
sample estimates:
prop 1 prop 2
0.1094606 0.3057366
Based on the result, p-value is much smaller than 0.05, we should reject . Female and Male do NOT have the same proportion
>50kof theclass
How to solve using z-test?
p1hat <- x12/(x11+x12) | |
p2hat <- x22/(x21+x22) | |
phat <- (x12+x22)/(x11+x12+x21+x22) | |
#get z statistic | |
zvalue <- (p1hat-p2hat)/(sqrt(phat*(1-phat)*(1/(x11+x12)+1/(x21+x22)))) | |
zvalue |
[1] -38.9729
#get critical region | |
alpha <- 0.05 | |
zalpha <- qnorm(1-alpha) | |
zalpha |
[1] 1.644854
#get p-value | |
pnorm(zvalue) #why? |
[1] 0
p-value is close to 0, we should reject .