# 理论基础:如何做人工智能机器学习研究?
# 医疗大数据 Medical Data
一般指的是所有与医疗以及健康相关的数据,都是医疗大数据。
医疗大数据来源:
- 医疗过程中
- 临床数据:病理自动录入,自动化诊断,治疗方法选择,预后判断
- 检查化验:化验检查结果自动化解读
- 实验室研究
- 新型的医疗数据,基因组学
- 组学概念:基因组学、蛋白质组学、代谢组学
- 影像组学:分析更多的特征,建立影像与疾病之间特异性的联系
- 现代管理,手环
# 人工智能 Artificial Intelligence
人工智能是计算机科学的一个分支,它企图了解智能的实质,并生产出一种新的能以人类智能相似的方式做出反应的智能机器,该领域的研究包括机器人、语言识别、图像识别、自然语言处理和专家系统等。
- 人工智能就是一个数据处理的过程
- 人工智能的问题本质是数学 —— 算法的问题
- 为什么谈到大数据就谈到人工智能?
因为大数据尤其适合用人工智能的方法来分析。
# 人工智能、机器学习、深度学习的关系
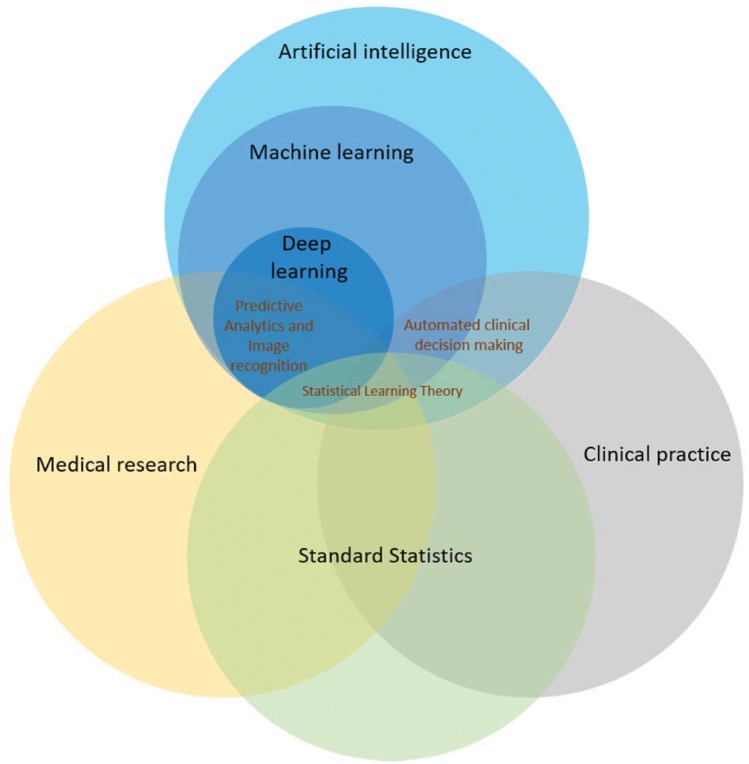
- 一般谈人工智能主要就是指机器学习
- 机器学习包含深度学习,采用算法不同
- 机器学习(人工智能)算法与传统统计分析有交叉
# 为什么大数据分析不用传统统计方法?
- 对数据结构、类型有比较严格的规定
- 很难整合全部数据做出完整分析
- 数据分析容量较小
- 并不是机器学习就一定比传统统计分析方法好!
# 机器学习一般实现过程
- 收集数据
最耗时
明确问题,课题设计,筛选收集的数据类型及指标 - 导入数据
将收集好的数据导入软件或 “工具” - 特征工程
数据处理:数据筛选,特征预处理 - 算法分析
采用算法对数据进行学习分析 - 得出结果
得到模型或分类结果
# 机器学习分类
# Supervised Learning 有监督学习
有监督学习的过程就是先通过已知的训练样本(已知输入和对应的输出) 让计算机( 算法) 进行 “学习”“训练”,可以得到一个最优模型,再将这个模型应用在新的数据上,这个模型可以根据输入的内容判断结果,模型就有了预知能力。有监督机器学习又被称为 “有老师的学习”,所谓的老师就是标签。
# Unsupervised Learning 无监督学习
无监督机器学习被称为 “没有老师的学习”,无监督相比于有监督,没有训练的过程,而是直接拿数据进行建模分析,分析的结果一般即分类结果。
# 工具基础:轻松入门 Python 与 Python 安装
# 安装 Python
- Anaconda
- Anaconda 指的是一个开源的 Python 发行版本,其包含了 conda、Python 等 180 多个科学包及其依赖项。因为包含了大量的科学包,Anaconda 的下载文件比较大。
- Jupyter Notebook
- 此前被称为 IPython notebook,是一个交互式笔记本,支持运行 40 多种编程语言。用于创建和共享文学化程序文档,支持实时代码,数学方程,可视化和 markdown。 用途包括:数据清理和转换,数值模拟,统计建模,机器学习等等。
# 常用 Python 包
- Numpy
- Numerical Python 是 Python 的一种开源的数值计算扩展。这种工具可用来存储和处理大型矩阵,比 Python 自身的嵌套列表
nested list structure结构要高效的多(该结构也可以用来表示矩阵matrix),支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库 - Pandas
- 是基于 NumPy 的一种工具,该工具是为了解决数据分析任务而创建的。Pandas 纳入了大量库和一些标准的数据模型,提供了高效地操作大型数据集所需的工具。Pandas 提供了大量能使我们快速便捷地处理数据的函数和方法。
Numpy/Pandas 是数据操作的基础。将数据导入 Python 时,数据以哪种格式保存,不同文件里的数据合并,按列排序,查找数据等。
- Scikit-learn
- 基于 SciPy,专门面向机器学习的 “工具包” Scikit-learn。 Scikitlearn 的基本功能主要被分为六大部分:分类,回归,聚类,数据降维,模型选择和数据预处理。
用来做特征工程、数据清洗与标准化等,以及建模用的数学命令。
- Keras\Tensorflow\Pytorch
- Keras 是一个由 Python 编写的开源人工神经网络库, 可以作为 Tensorflow、Microsoft-CNTK 和 Theano 的高阶应用程序接口,进行深度学习模型的设计、调试、评估、应用和可视化
- TensorFlow 是一个基于数据流编程的符号数学系统,被广泛应用于各类机器学习(machine learning)算法的编程实现。
- PyTorch 是一个开源的 Python 机器学习库,基于 Torch,用于自然语言处理等应用程序。
深度学习的 3 个库
Keras 简单一些,TensorFlow 是谷歌出品,较难较复杂
PyTorch 介于两者之间
其他:
- Matplotlib:作图
- Statsmodels:统计分析,代替 SPSS
- OpenCV:处理图片
- NLTK:自然语言处理
# 常用算法
K-Nearest Neighbor, KNN
K 近邻Decision Tree
決策树
一个起点,根据不同情况画出不同的分支Random Forest
随机森林
建立不同的决策树,每个决策树都有不同的结果,对这些决策树进行投票,选择票数最多的一个Support Vector Machine, SVM
支持向量机Logistic/LASSO/ Ridge regression
逻辑回归 / LASSO 回归/岭回归BayeS
贝叶斯算法
概率论领域中发展出来的
现在多用于垃圾邮件分类Convolutional Neural Networks, CNN/Recurrent Neural Network, RNN
卷积神经网络 / 循环神经网络
以上算法都是用来解决有监督学习问题,用来解决分类、回归等
比如疾病诊断、心电图超声自动诊断等
- Clustering method:K-means/DBSCN
聚类算法:K-means/DBSCN
用来做无监督学习
# 有监督学习实操:用 Python 做机器学习代码演示
打开 Anaconda,找到 Notebook,选择 Launch
#导入常用包 | |
import numpy as np | |
import pandas as pd | |
#导入数据 | |
data = pd.read_csv('Prostate_Cancer.csv') | |
#数据信息 | |
data.info() | |
#数据前 5(10)项 | |
data.head(10) | |
#选取自变量 | |
data.iloc[:,2:] | |
#建立索引的一种方式 | |
#data.iloc [起始行号:结束行号,起始列号:结束列号] | |
#留空是指每一行 / 列都要 | |
#行号 / 列号从 0 开始 | |
#定义自变量和因变量 | |
X =data.iloc[:,2:] | |
y =data['diagnosis_result'] | |
#导入 Scikit-learn 的数据拆分模块 train_test_split | |
from sklearn.model_selection import train_test_split | |
#拆分数据集 | |
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size = 0.3, random_state = 99) | |
#训练集 X,测试集 X,训练集 y,测试集 y | |
#test_size = 0.3 测试集给 30% 的数据 | |
#random_state = 99 随机拆分,随机条件限定为 99,每次结果均一样;可删除,删除后每次运行结果不一样 | |
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape) | |
#导入 Logistic 模型 | |
from sklearn.linear_model import LogisticRegression | |
from sklearn import metrics | |
#训练模型 | |
model_Log = LogisticRegression() | |
model_Log.fit(train_X, train_y) | |
#预测测试集 | |
prediction_Log = model_Log.predict(test_X) | |
#输出 | |
prediction_Log | |
#Series 变成 ndarray 格式 | |
test_y_nd=np.array(test_y) | |
test_y_nd | |
#计算准确率 | |
metrics.accuracy_score(prediction_Log,test_y) | |
#结果:0.9 | |
#换一种模型试试 | |
#导入 KNN 模型 | |
from sklearn.neighbors import KNeighborsClassifier | |
#训练模型 | |
model_KNN=KNeighborsClassifier(n_neighbors=10) | |
#n_neighbors=10 是设定的参数 | |
model_KNN.fit(train_X, train_y) | |
#预测测试集 | |
prediction_KNN = model_KNN.predict(test_X) | |
#计算准确率 | |
metrics.accuracy_score(prediction_KNN,test_y) | |
#结果:0.833333333334 | |
#假设新来一个病人 | |
example=[[ 20, 13, 140, 940, 0.146, 0.278, 0.240, 0.056]] | |
#用训练好的 model_KNN 模型来测试一下 example 的结果,看良恶性 | |
prediction_ex = model_KNN.predict(example) | |
prediction_ex |
# 数据处理基础:数据预处理(Feature-engineering 特征工程)和数据降维
数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。
特征工程就是通过一系列办法最大限度地从原始数据中提取特征以供算法和模型使用。
- 特征筛选:数据清洗,特征选择
- 数据预处理:
- 标准化
利用平均数和标准差,将数值大小缩放到 0 附近
标准差 σ 肯定为正数,当 x 大于平均数时,x' 为正数,小于平均数时,x' 为负数,以此缩放到 0 附近- 归一化
将数值缩放到了 0 - 1 之间
# 矩阵与矩阵乘法
- 矩阵
Matrix - 由 m×n 个数 aij 排成的 m 行 n 列的数表称为 m 行 n 列的矩阵,简称 m×n 矩阵。记作:
这 m×n 个数称为矩阵 A 的元素,简称为元,数 aij 位于矩阵 A 的第 i 行第 j 列,称为矩阵 A 的 (i,j) 元,以数 aij 为 (i,j) 元的矩阵可记为 (aij) 或 (aij) m×n,m×n 矩阵 A 也记作 Amn。
- 矩阵乘法
- 两个矩阵的乘法仅当第一个矩阵 A 的列数和另一个矩阵 B 的行数相等时才能定义。如 A 是 m×n 矩阵和 B 是 n×p 矩阵,它们的乘积 C 是一个 m×p 矩阵 ,它的一个元素:
并将此乘积记为:
例如:
相乘后的矩阵行列,分别取决于第一个矩阵的行和第二个矩阵的列
- 矩阵可以用来储存信息
- 我们的数据在电脑上就是矩阵的形式
- 我们对数据进行各种操作运算,其实就在进行矩阵运算和其他各种运算
举例 1:简单矩阵 2*3
原始数据:思考:添加标签
| 体重 | 身高 | 血红蛋白 | |
|---|---|---|---|
| 病人 A | 75 | 1.80 | 90 |
| 病人 B | 80 | 1.70 | 120 |
简单矩阵 2 行 * 3 列 × 3 行 * 2 列的矩阵 = 2 行 * 2 列
原始数据再加上一列 血糖 值和一列 肌酐 值
再加上一行 病人 C
| 体重 | 身高 | 血红蛋白 | 血糖 | 肌酐 | |
|---|---|---|---|---|---|
| 病人 A | 75 | 1.80 | 90 | 6.0 | 60 |
| 病人 B | 80 | 1.70 | 120 | 8.0 | 50 |
| 病人 C | 100 | 2.00 | 100 | 10.0 | 50 |
复杂矩阵 3 行 * 5 列 × 5 行 *2 列的矩阵 = 3 行 * 2 列
# 数据降维 - PCA(主成分分析)
- 原始数据中每个对象的特征包括很多维度,无法直观展示
- 通过矩阵运算,将原始数据的多个维度可以转换成两个维度,并且转换后的数据与原始数据间有一一对应的关系,可以在直角坐标系中展示
- 矩阵的选择标准:可以突显原始数据中每个对象之间的差别,我们使其在直角坐标系中的相互距离最远
# 无监督学习实操: 用 Python 做特征工程与数据降维代码演示
# 数据标准化示例
#导入标准化模块 | |
from sklearn.preprocessing import StandardScaler | |
#定义转换器 | |
transfer=StandardScaler() | |
#转换前的数据 | |
train_X | |
#标准化训练集里的数据 | |
train_X_SS = transfer.fit_transform(train_X) | |
#转换后的数据 | |
train_X_SS | |
#转换为 ndarray 格式,二维矩阵 | |
#转换后的数据 “形状” | |
train_X_SS.shape | |
#ndarray 格式转换为 DataFrame 格式 | |
train_x_SS_df=pd.DataFrame(train_X_SS) | |
train_x_SS_df | |
#输出一个表格 | |
#标准化测试集里的数据 | |
test_X_SS = transfer.fit_transform(test_X) | |
test_X_SS | |
#训练 KNN 模型 | |
model_KNN_SS=KNeighborsClassifier(n_neighbors=10) | |
model_KNN_SS.fit(train_X_SS, train_y) | |
#预测测试集 | |
prediction_KNN_SS = model_KNN_SS.predict(test_X_SS) | |
#计算准确率 | |
metrics.accuracy_score(prediction_KNN_SS,test_y) | |
#0.9333333 | |
#数值有提升 | |
#训练 Logistic 模型 | |
model_Log_SS = LogisticRegression() | |
model_Log_SS.fit(train_X_SS, train_y) | |
#预测测试集 | |
prediction_Log_SS = model_Log_SS.predict(test_X_SS) | |
#计算准确率 | |
metrics.accuracy_score(prediction_Log_SS,test_y) | |
#0.9 | |
#没有变化,标准化后对该模型的结果没有改变 |
# 数据降维
import numpy as np | |
import pandas as pd | |
#data 存储原始数据 | |
data = pd.read_csv('Prostate_Cancer.csv') | |
data.head(10) | |
X =data.iloc[:,2:] | |
y =data['diagnosis_result'] | |
#导入降维模块 | |
from sklearn import decomposition | |
#降维后的数据定为二维 | |
pca = decomposition.PCA(n_components=2) | |
#进行数据转换 | |
reduced_X = pca.fit_transform(X) | |
reduced_X | |
reduced_X.shape | |
#(100,2) 100 行 2 列 | |
#横坐标 | |
x = reduced_X[:,0] | |
#100 行都要,0 是指第一列 | |
x | |
#纵坐标 | |
y = reduced_X[:,1] | |
#100 行都要,1 是指第二列 | |
y | |
#导入画图的包 | |
import matplotlib.pyplot as plt | |
#画图 | |
plt.scatter(x,y) |
# 无监督学习
#导入 KMeans 算法 | |
from sklearn.cluster import KMeans | |
#聚成 3 类 | |
kms = KMeans(n_clusters=3) | |
#用算法分类降维后的数据 | |
cluster = kms.fit_predict(reduced_X) | |
cluster | |
#分成了 0,1,2 三类 | |
cluster.shape | |
#(100,) | |
#数据集里的每个值是否等于 0,返回 true 或 false | |
cluster==0 | |
#x 是数据转换后的横坐标 | |
x[cluster==0] | |
#挑选出符合 true 的数据,即挑选出 0 组的数据 | |
#y 是数据转换后的纵坐标 | |
y[cluster==0] | |
#开始画图 | |
plt.figure() | |
#0 组数据的横坐标,0 组数据的纵坐标,颜色用红色 | |
plt.scatter(x[cluster==0],y[cluster==0],color='r') | |
#1 组数据的横坐标,1 组数据的纵坐标,颜色用蓝色 | |
plt.scatter(x[cluster==1],y[cluster==1],color='b') | |
#2 组数据的横坐标,2 组数据的纵坐标,颜色用绿色 | |
plt.scatter(x[cluster==2],y[cluster==2],color='g') | |
#处理原始数据集 data | |
#原始数据中符合 0 组的 | |
data[cluster==0] | |
data[cluster==1] | |
data[cluster==2] | |
data[cluster==0].shape | |
data[cluster==1].shape | |
data[cluster==2].shape | |
#分组数据导出到 excel | |
data[cluster==2].to_excel('cluster2.xlsx') |
# Python 人工智能学习路线
# 初学
红色石头
哔哩哔哩,千锋教育,Python 机器学习课程
Python\Numpy\Pandas\Scikit-learn\Git-hub
天池大数据平台、Kaggle
# 进阶学习
- 数学基础:
- 数学基础《程序员的数学》
- 机器学习 —— 数学基础视频课程
- 李航《统计学习方法》,周志华《机器学习》
- 机器学习:
- 吴恩达、林轩田课程
- 《利用 Python 进行数据分析》
- 机器学习 “四大名著”